So, you're thinking about taking the College Algebra CLEP exam? Awesome! Here's what you need to know.
You’ll have 60 questions to answer in 90 minutes and you’ll be examined on what you usually learn in an algebra course in one semester at college. The topics will include basic algebraic operations; equations, inequalities, and graphs of various types, including linear and quadratic ones; functions of various types, including algebraic, exponential and logarithmic ones; and various other topics. 50% of the test is about simple problems, where you’ll only need your basic algebra skills. The other 50% is about more complex problems, where you’ll have to apply algebra concepts that you’ve learnt, to show that you understand the concepts. You won’t be examined on arithmetic calculations as such. However, you should be already conversant with algebraic vocabulary, symbols, and notation. Moreover, there will be an online non-graphing scientific calculator at your disposal during the test.
If you've previously studied algebra during high school or through extracurriculars, you'll likely find this test pleasantly fast. If not, you can study through it in no time and be up and running. It's probably one of the easiest Mathematics CLEP exams but be careful to not underestimate it!
The exam will be divided into four major chunks:
Algebraic operations are at the core of Mathematics. Everything you do in Mathematics will involve algebraic operations, which shows the importance of this section. This section is relatively easy and will set the foundation for the following ones. Here, you’ll learn how to apply the algebraic operations (addition, subtraction, multiplication, and division) to various forms of algebraic expressions.
You’ll first learn about polynomials and how to factor them, i.e. express them as a product of other expressions, and expand them, i.e. construct them from that product. Then, you’ll look into expressions involving concepts such as real numbers, rational numbers, fractions, exponents, scientific notation, roots, radicals, denominators and rationalization, rational expressions and compound fractions, and how to simplify those expressions, all while keeping in mind the order of operations. Finally, you’ll understand logarithms, how to use their properties to expand and simplify logarithmic expressions, how to change the base of logarithms and how they relate to exponents.
All of this section will help you not only in Mathematics but in various other fields like Science, Engineering, Economics and even Medicine. So, learn your algebra!
Solving equations and inequalities is one of the most essential skills in algebra: countless realworld problems make use of it. This section will show you how to solve various types of equations and inequalities. Before you delve into this, you’ll need to understand the difference between equations and inequalities and how to rewrite equations by changing the subject of formula.
First, you’ll solve linear equations and inequalities, which is very straightforward. You’ll then solve quadratic equations and inequalities, using factoring, square root property, completing the square, quadratic formula, and graphing which you’ll learn in the next section. Next, you’ll need to understand what absolute values are and how to rewrite absolute value expressions without the absolute value sign, so that you can solve absolute value equations and inequalities just like the usual ones. You’ll also solve systems of equations and inequalities, using graphing, substitution and elimination. Finally, you’ll solve exponential and logarithmic equations using the properties of logarithms and the exponent-logarithm relationship that you’ll have learnt in the previous section.
After this section, you'll be able to tackle real-world applications involving all those types of equations and inequalities. Those applications range from numbers, geometry, statistics, and economics, to science, construction, navigation, architecture, and transportation, through music, psychology, and energy, among many others.
Functions are one of the most important concepts in Mathematics: they help you to build models to simulate real-world problems and find out the output of a situation given a certain input, for example, the return on investment of $10,000 at an annual rate of 3% over a given number of years. This section is the biggest, but don’t worry: practice and you’ll get it! Keep in mind that the functions that you’ll encounter in this section will vary among all the different types of functions that you’ll have learnt in the course, including linear, polynomial, rational, absolute value, power, exponential, logarithmic and piecewise-defined.
Once you understand what functions are and the function notation, you’ll learn how to interpret the various forms in which functions can be represented (graphs, tables, equations, and words). To better understand functions, at this point, it will be helpful to have a look at examples of some applications of functions that model real-world problems. You’ll also learn about domain and range, and how to find out the domain of a function, which will be necessary when graphing functions. Most importantly, since the essence of a function is to find the output given an input, you’ll evaluate functions. Moreover, this being an algebra course, you’ll apply algebraic operations to functions in order to find sum, difference, product and quotient functions, and you’ll combine functions, using composition. Furthermore, if you have to solve a complex model, wouldn’t it be helpful to visualize the functions? Drawing graphs comes in handy here. After going over graph concepts (cartesian coordinate system and point plotting) and graph properties (including symmetry), you’ll be able to find the domain and range of a function from its graph. Sometimes, algebraic operations also need to be performed on graphs, too. To understand how applying an operation to a function changes it, and how this consequently changes its graph, you’ll learn about graph transformations, such as shift, reflection, stretch and shrink. Finally, what if you want to know for how long you need to invest $10,000 at a rate of 3% to get a given return? To interchange the input and output of a function, you’ll find its inverse. You’ll also have to know about the properties of inverse functions and the graph relationship between a function and its inverse.
You’ll be able to apply all this knowledge in constructing and simulating models of real-world problems. For instance, if you are an entrepreneur and are wondering about how much profit you can make given a price, you can construct a model with functions for demand, cost, and revenue, and use these to create a function of price for profit. How cool is that?
Can you imagine Mathematics without numbers? Indeed, number systems are at the heart of Mathematics! This section is the fastest and you’ll go over basic concepts of number systems and operations involving them.
A number system that you’ll study is real numbers, along with their properties. The other number system is complex numbers: once you understand what they are and how they relate to radicals, you’ll rewrite in standard form expressions containing them, apply algebraic operations to them and solve equations containing them. You’ll also learn about sequences, find the term in any position in a sequence, form a series from a sequence and write a series in summation notation as well as the other way around. In addition to this, you'll discover counting techniques involving addition: you'll study two special types of sequences, arithmetic and geometric, and, using their sum formulas, you'll find the sum of any number of terms in their series, without having to add every single number. Counting techniques involving multiplication are on the menu as well. How can you find the product of numbers from 1 to n without having to multiply every single number in between? Factorials! How about expanding expressions in the form of (𝑎 + 𝑏) 𝑛 without multiplying (𝑎 + 𝑏) by itself for 𝑛 times? Binomial theorem! Finally, you’ll have a brief look at calculating the determinant of a 2x2 matrix, which is an important concept in more advanced topics involving matrices.
Fun fact: did you know that the complex number 𝑖 was invented just because there was no answer to √−1?
Correct Answer: A. 4x(x+1)(x-1)(3x-2)
Explanation: This one is fairly easy. However, you’ll have to remember the difference of squares: x^2-y^2=(x+y)(x-y). 12x^4-8x^3-12x^2+8x=4x(3x^3-2x^2-3x+2) =4x(x^2 (3x-2)-1(3x-2)) =4x(x^2-1)(3x-2) =4x(x+1)(x-1)(3x-2) Note that x^2-1=x^2-1^2, which is a difference of squares.
Correct Answer: B. log((x^2 y^3)/z)
Explanation: For this question, you’ll need to recall some of the properties of logarithms: log_b (xy)=log_(b ) x+log_(b ) y log_b (x/y)=log_(b ) x-log_b y log_b〖y^x=〖x log_b〗y 〗 2 logx+3 logy-logz=log〖x^2+log y^3-log z〗 =log(x^2 y^3 )-logz =log((x^2 y^3)/z)
Correct Answer: A. x≥3.24
Explanation: (6x-4)/3-2≥ 8-3x/2 (6x-4)/3+3x/2≥8+2 (2(6x-4)+3(3x))/6≥10 (12x-8+9x)/6≥10 (21x-8)/6≥10 21x-8≥10×6 21x≥68 x≥68/21 or 3.238095 ≈3.24 (to 2 d.p.)
Correct Answer: D. (4±√106)/10
Explanation: You guessed it: whenever a quadratic equation looks complex enough while solving, the safest way to go about it is the quadratic formula (-b±√(b^2-4ac))/2a. 4x+7/2=5x^2-1 5x^2-4x-1-7/2=0 10x^2-8x-9=0 x=(-(-8)±√((-8)^2-4(10)(-9) ))/2(10) =(8±√424)/20 =(8±√4x106)/20 =(4±√106)/10
Correct Answer: D. x=1,e^2,e^(-2)
Explanation: When solving logarithmic equations, you’ll often use the properties of logarithms. For this particular question, don’t forget that while log_by^2=2 log_by , (log_by)^2=(log_by )(log_by). (ln x)^3=ln x^4 (ln x)^3-ln x^4=0 (ln x)^3-4 ln x=0 ln x ((ln x)^2-4)=0 ln x=0 x=e^0 =1 (lnx)^2-4=0 (lnx)^2=4 lnx= ±√4 =±2 lnx=2 x= e^2 lnx=-2 x=e^(-2)
Correct Answer: B. 729
Explanation: This question is another easy one. You'll use the concept of composition of functions, where you apply functions consecutively. All you have to keep in mind is the order in which the functions are to be applied: the first function in the notation is, in fact, the second function to be applied. Then, you'll simply have to evaluate the resulting combined function. fg(3)=f(g(3)). Therefore, first consider g(x). g(x)=x^2-x+3 Proceed to use g(x) to evaluate f. f(g(x))=f(x^2-x+3) f(x)=x^3 ∴f(x^2-x+3)=(x^2-x+3)^3 f(g(x))=(x^2-x+3)^3 ∴fg(3)=(3^2-3+3)^3 =729
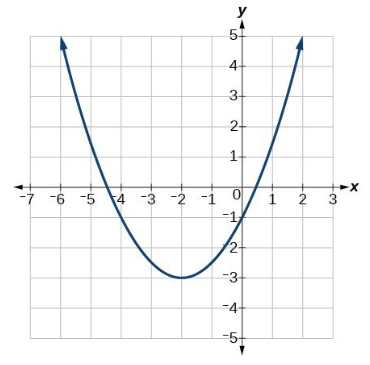
Correct Answer: D. 1/2 x^2+2x-1
Explanation: At first, this one looks difficult, but if you know the properties of graphs – especially quadratic – well, you’ll find the answer without any calculations: for a quadratic graph y=ax^2+bx+c, if a>0, the vertex is a minimum and the graph therefore has U-shape. Similarly, if a<0, the vertex is a maximum and the graph has an upside-down U-shape. Wasn’t this one super easy?
Correct Answer: D. √(x-5),x≥5
Explanation: x≥0 (domain of f(x)) ∴f(0)≥5 (range of f(x)) Replace f(x) with y, interchange x and y, then make y the subject of formula. y=x^2+5 x=y^2+5 y^2=x-5 y=±√(x-5) f^(-1) (x)=±√(x-5) √(x-5) cannot be negative – what about the complex number i, you ask? Yes, you indeed studied complex numbers, but, in this section, they don’t have their place. ∴√(x-5) ≥0 x-5≥0 x≥5 (domain of f^(-1) (x)) Moreover, since the domain of f(x) is greater than 0, the range of f^(-1) (x) must also be greater than 0. Because of this, we discard the negative sign before √(x-5). The final answer thus becomes f^(-1) (x)=√(x-5),x≥5.
Correct Answer: D. z=1-4i
Explanation: If you’re wondering what is i, check out the fun fact at the end of the last section of the study guide. You’ll also have to use conjugates, here. Just for a quick refresher, the conjugate of x-ci is simply x+ci. First, make z the subject of formula in the equation. (6+4i)z+12i-6=16-8i (6+4i)z=16-8i-12i+6 =22-20i Then, multiply the numerator and the denominator by the conjugate of the denominator. z=(22-20i)/(6+4i) =(22-20i)/(6+4i)×(6-4i)/(6-4i) =((22-20i)(6-4i))/(6+4i)(6-4i) =(22(6)-22(4i)-6(20i)+(20i)(4i))/(6^2-6(4i)+6(4i)-(4i)^2 ) =(132-88i-120i+80i^2)/(36-16i^2 ) =(132-208i+80(-1))/(36-16(-1) ) =(52-208i)/52 =1-4i
Correct Answer: C. 28
Explanation: Although this one may seem tedious, it’s not – as long as you remember the binomial theorem! To find the term containing x^k in (x+c)^n, the binomial formula is (n/(n-k)) x^k c^(n-k). (x-1)^8=(8/(8-6)) x^6 × (-1)^(8-6) =((8/2) x^6 × (-1)^2 =28×x^6× 1 =28 x^6 So, the coefficient of x^6 is 28. Simple, right?
While quite short on the study side of things, the official CLEP book is the go-to final practice test. Since this is the only official practice test available, I normally use it as my final spot check before taking the test.
Textbooks are great as far as they go, but I’d generally recommend you opt for this exam guide instead. It tends to cut through the confusion and help you accelerate your learning process.
The website looks like it was made before the internet, but it’s legitimately the single most useful study guide I’ve found yet. Basically it’s a series of flashcards that help you study in a fast paced and fun way.